Combining Multivariate Time Series and Derivatives Analytics¶
Data Science Luxembourg, 10.02.2016
Dr. Yves J. Hilpisch
The Python Quants GmbH
Aboute Me¶





For the curious:
- http://tpq.io (company Web site)
- http://pqp.io (Quant Platform)
- http://datapark.io (data science in the browser)
- http://fpq.io (For Python Quants conference)
- http://meetup.com/Python-for-Quant-Finance-London/ (1,200+ members)
- http://pff.tpq.io | http://dawp.tpq.io | http://lvvd.tpq.io
- http://hilpisch.com (all my talks and more)
- http://twitter.com/dyjh (events, talks, finance news)
Multivariate Vector Auto Regression with R¶
Processing the Data with Python¶
As an illustrative example we are going to analyze index data for the EURO STOXX 50 stock index and its volatility index VSTOXX. First, some Python imports.
import numpy as np
import pandas as pd
import seaborn as sns; sns.set()
%matplotlib inline
%load_ext rpy2.ipython
import warnings; warnings.simplefilter('ignore')
Second, some R imports.
%%R
library('zoo')
library('xts')
library('vars')
STOXX Limited provides open data for the two indicies on their Web site. We start with the VSTOXX data.
vs_url = 'http://www.stoxx.com/download/historical_values/h_vstoxx.txt'
vs = pd.read_csv(vs_url, # filename
index_col=0, # index column (dates)
parse_dates=True, # parse date information
dayfirst=True, # day before month
header=2) # header/column names
vs = vs.resample('MS') # resampling to month start frequency
A quick look at the most recent data rows.
vs.tail()
| V2TX | V6I1 | V6I2 | V6I3 | V6I4 | V6I5 | V6I6 | V6I7 | V6I8 | |
|---|---|---|---|---|---|---|---|---|---|
| Date | |||||||||
| 2015-10-01 | 23.650945 | 23.610630 | 24.053955 | 24.104005 | 24.420600 | 24.953082 | 25.060995 | 25.282791 | 25.778995 |
| 2015-11-01 | 22.819967 | 22.048163 | 22.769295 | 22.446665 | 23.512514 | 24.191938 | 24.377910 | 24.622286 | 25.236167 |
| 2015-12-01 | 23.773375 | 27.789483 | 23.793500 | 24.163295 | 24.787850 | 25.179785 | 25.328595 | 25.543580 | 25.921474 |
| 2016-01-01 | 29.650480 | 30.799394 | 29.462415 | 28.658326 | 28.718210 | 28.152100 | 27.895670 | 27.711790 | 27.275525 |
| 2016-02-01 | 29.383320 | 28.933540 | 29.541060 | 28.858660 | 29.054280 | 28.685680 | 28.659340 | 28.612700 | 28.353340 |
We write a sub-set of the data to disk as a CSV file.
vs[['V2TX', 'V6I4', 'V6I8']].to_csv('v2tx.csv')
VAR for the VSTOXX¶
The data can be read easily with R.
%%R
vd <- read.csv('v2tx.csv')
data <- xts(vd[, -1], as.POSIXct(as.character(vd[,1]), format="%Y-%m-%d"))
Next, we generate a multivariate VAR model in R.
%R mod <- VAR(data, p=12, season=12, type='both');
Fitting of the main index.
%R plot(mod, names='V2TX')
Fitting of two sub-indices (I).
%R plot(mod, names='V6I4')
Fitting of two sub-indices (II).
%R plot(mod, names='V6I8')
Finally, a forecast over 60 months.
%%R
pr = predict(mod, n.ahead=60, ci=0.9, dumvar = NULL)
plot(pr)
Combining VSTOXX & EURO STOXX 50¶
Retrieval of the EURO STOXX 50 data is a bit more involved.
cols = ['Date', 'SX5P', 'SX5E', 'SXXP', 'SXXE',
'SXXF', 'SXXA', 'DK5F', 'DKXF', 'DEL']
es_url = 'http://www.stoxx.com/download/historical_values/hbrbcpe.txt'
es = pd.read_csv(es_url, # filename
header=None, # ignore column names
index_col=0, # index column (dates)
parse_dates=True, # parse these dates
dayfirst=True, # format of dates
skiprows=4, # ignore these rows
sep=';', # data separator
names=cols) # use these column names
# deleting the helper column
del es['DEL']
We generate a new data set for the two main indices.
es = es.resample('MS') # resampling to month start
data = vs.join(es)[['V2TX', 'SX5E']]
data.corr()
| V2TX | SX5E | |
|---|---|---|
| V2TX | 1.000000 | -0.334486 |
| SX5E | -0.334486 | 1.000000 |
In what follows, we work with normalized data.
data = data / data.ix[0] * 100
data.tail()
| V2TX | SX5E | |
|---|---|---|
| Date | ||
| 2015-10-01 | 65.470679 | 93.253030 |
| 2015-11-01 | 63.170358 | 97.924786 |
| 2015-12-01 | 65.809589 | 93.627527 |
| 2016-01-01 | 82.078623 | 86.278605 |
| 2016-02-01 | 81.339070 | 83.441038 |
A plot of the data.
data.plot(figsize=(10, 6), subplots=True, color='b');
We write a sub-set of the data again as CSV file to disk.
data[data.index >= '2005-1-1'].to_csv('v2tx_sx5e.csv')
As before, the data stored as CSV file is read into an R object.
%%R
vd <- read.csv('v2tx_sx5e.csv')
data <- xts(vd[, -1], as.POSIXct(as.character(vd[,1]), format="%Y-%m-%d"))
The VAR model and a plot for the stock index.
%R mod <- VAR(data, p=12, season=12, type='both');
%R plot(mod, names='SX5E')
The forecast over a 60 months period with a 90% confidence interval.
%%R
pr = predict(mod, n.ahead=60, ci=0.9, dumvar = NULL)
plot(pr)
Finally, an impulse response analysis.
%%R
ir <- irf(mod, impulse = NULL, response = NULL, n.ahead = 48,
ortho = TRUE, cumulative = FALSE, boot = TRUE, ci = 0.90,
runs = 100, seed = NULL)
The graphical representation of the IRA results.
%R plot(ir)
Hit <Return> to see next plot:
Model Calibration Data¶
Derivatives Model Calibration¶
Model calibration is a numerical optimization routine that looks for such parameters for a given model that best replicate market observed option quotes.
In our case, we fit a square-root diffusion (CIR) process with 3 parameters to options on the VSTOXX volatility index.
$$dv_t = \kappa (\theta - v_t) dt + \sigma \sqrt{v_t} dZ_t$$%run dx_srd_calibration.py
parameters.set_index('date').to_csv('srd_parameters.csv')
A possible calibration result might look as follows.
from IPython.display import Image
Image('calibration_result.png', width='75%')
The Data¶
We import the data set ...
para = pd.read_csv('srd_parameters.csv', index_col=0, parse_dates=True)
para[['initial_value', 'kappa', 'theta', 'sigma', 'MSE']].head()
| initial_value | kappa | theta | sigma | MSE | |
|---|---|---|---|---|---|
| date | |||||
| 2014-01-02 | 18.9286 | 2.735729 | 17.313088 | 3.553804 | 0.002043 |
| 2014-01-03 | 18.0018 | 2.687111 | 17.415745 | 3.648552 | 0.001941 |
| 2014-01-06 | 18.1672 | 2.684570 | 17.438809 | 3.639782 | 0.002013 |
| 2014-01-07 | 17.1932 | 2.711549 | 17.644289 | 3.608929 | 0.004547 |
| 2014-01-08 | 17.3671 | 2.737476 | 17.841848 | 3.592961 | 0.003493 |
... and plot it.
para[['initial_value', 'kappa', 'theta', 'sigma', 'MSE']].plot(
figsize=(10, 12), subplots=True, color='b');
VAR Model for the Calibration Data¶
Setting up the VAR Model¶
We write the relevant sub-set of the data to disk ...
para[['initial_value', 'kappa', 'theta', 'sigma']].to_csv('srd_para_for_r.csv')
... and read it with R.
%%R
vd <- read.csv('srd_para_for_r.csv')
data <- xts(vd[, -1], as.POSIXct(as.character(vd[, 1]), format="%Y-%m-%d"))
The VAR model based on the calibration data.
%R mod <- VAR(data, p=5, season=20, type='both');
For instance, theta shows a good fit.
%R plot(mod, names='theta')
Forecast for the Derivatives Model Parameters¶
We generate a forecast for 20 trading days.
%%R
pr = predict(mod, n.ahead=20, ci=0.9, dumvar = NULL)
plot(pr)
The forecast results are found in the fcst attribute.
%R attr(pr, 'names')
array(['fcst', 'endog', 'model', 'exo.fcst'],
dtype='|S8')
We pull the results to the Python run-time ...
%%R
ivs <- pr$fcst$initial_value
ks <- pr$fcst$kappa
ts <- pr$fcst$theta
ss <- pr$fcst$sigma
%R ivs[1:5]
array([ 15.09791646, 12.51026196, 12.1718373 , 11.15844494, 12.12437766])
%Rpull ivs
%Rpull ks
%Rpull ts
%Rpull ss
... and store them in a pandas DataFrame object.
index = pd.date_range(start='2014-4-1', periods=len(ivs), freq='B')
fc = pd.DataFrame({'initial_value' : ivs[:, 0],
'kappa' : ks[:, 0],
'theta' : ts[:, 0],
'sigma' : ss[:, 0]}, index=index)
The forecast results plotted with Python.
fc.plot(figsize=(10, 10), subplots=True, color='b');
DX Analytics¶
Background and Philosophy¶
DX Analytics is a Python library for advanced financial and derivatives analytics authored and maintained by The Python Quants. It is particularly suited to model multi-risk and exotic derivatives and to do a consistent valuation of complex derivatives portfolios. It mainly uses Monte Carlo simulation since it is the only numerical method capable of valuing and risk managing complex, multi-risk derivatives books.
DX Analytics is open source, cf. http://dx-analytics.com & http://github.com/yhilpisch/dx.
The development of the library is guided by two central principles.
- global valuation approach: in practice, this approach translates into the non-redundant modeling of all risk factors (e.g. option underlyings like equity indexes) and the valuation of all derivative instruments by a unique, consistent numerical method — which is Monte Carlo simulation in the case of DX Analytics
- unlimited computing resources: in 2016, the technical infrastructures available to even smaller players in the financial industry have reached performance levels that 10 years ago seemed impossible or at least financially not feasible; in that sense "unlimited resources" is not to be understood literally but rather as the guiding principle that hardware and computing resources generally are no longer a bottleneck
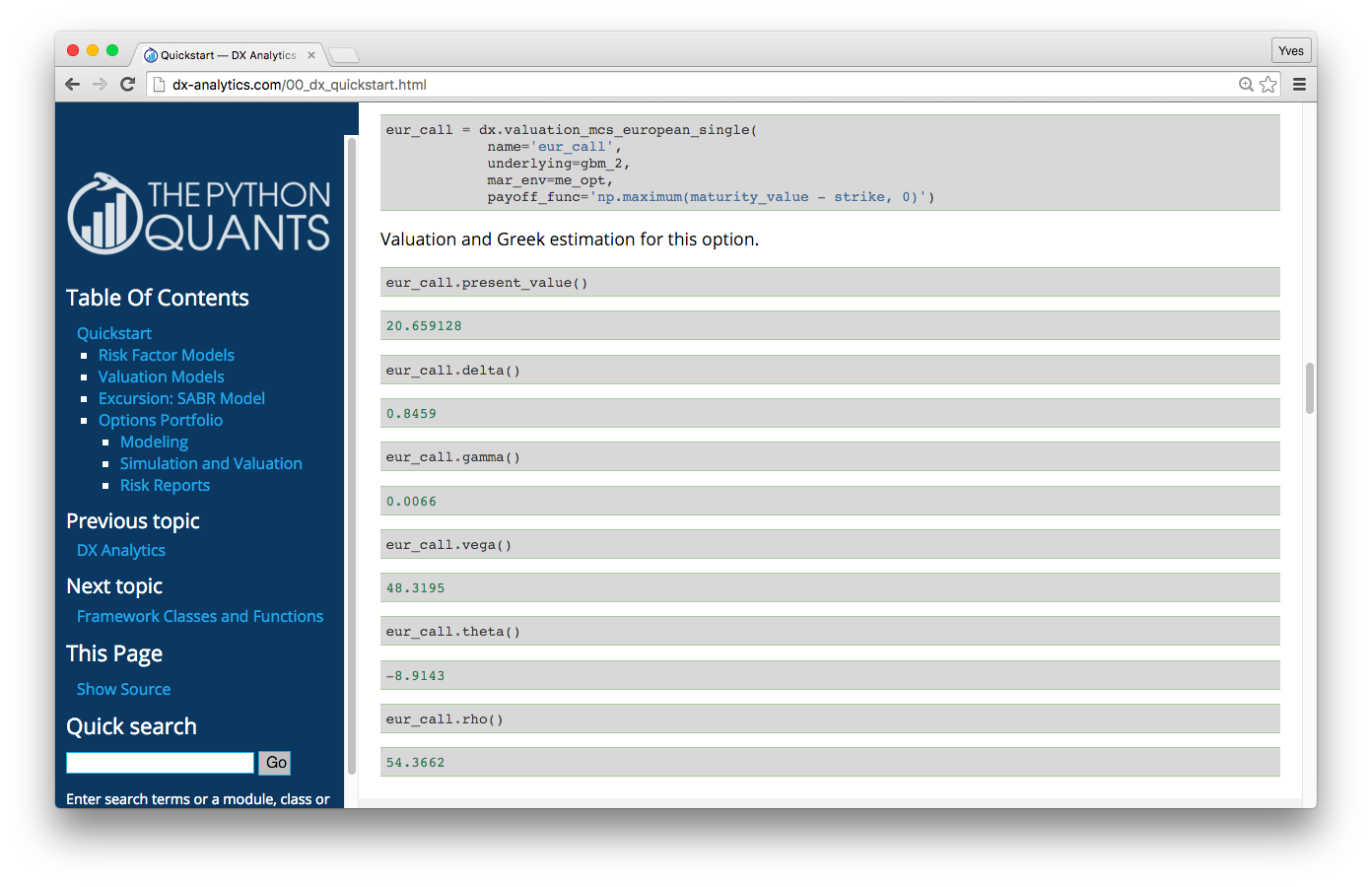
Example: DX Analytics — Quick Start
Example: DX Analytics — Complex
This example values a portfolio with 50 (correlated) risk factors and 250 options (European/American exercise) via Monte Carlo simulation in risk-neutral fashion with stochastic short rates.
http://dx-analytics.com/13_dx_quite_complex_portfolios.html
Modeling the VSTOXX Index¶
In what follows, we model the VSTOXX volatility index by a square-root diffusion process with DX Analytics. First, some imports.
import dx
import datetime as dt
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
All relevant data is stored in a market_environment object.
r = dx.constant_short_rate('r', 0.01)
me = dx.market_environment('me', para.index[0])
me.add_constant('initial_value', para['initial_value'].ix[0])
me.add_constant('kappa', para['kappa'].ix[0])
me.add_constant('theta', para['theta'].ix[0])
me.add_constant('volatility', para['sigma'].ix[0])
me.add_constant('final_date', dt.datetime(2014, 12, 31))
me.add_constant('currency', 'EUR')
me.add_constant('paths', 50000)
me.add_constant('frequency', 'W')
me.add_curve('discount_curve', r)
With this data, we instantiate the simulation object and simulate the process.
vstoxx = dx.square_root_diffusion('vstoxx', me)
paths = vstoxx.get_instrument_values()
The first 10 paths from the Monte Carlo simulation.
plt.figure(figsize=(10, 6));
plt.plot(vstoxx.time_grid, paths[:, :10]);
plt.gcf().autofmt_xdate();
Modeling a Derivative Instrument¶
In a next step, we instantiate a valuation object for a single-risk derivative instrument — in our case a European call option.
me.add_constant('strike', 15) # me.get_constant('initial_value'))
me.add_constant('maturity', me.get_constant('final_date'))
call = dx.valuation_mcs_european_single(name='call', underlying=vstoxx,
mar_env=me, payoff_func='np.maximum(maturity_value - strike, 0)')
The valuation takes then only a single method call.
call.present_value()
3.774749
Let us do several valuations for different strikes.
call_values = []
strikes = np.linspace(10, 30, 20)
orig_strike = call.strike
for k in strikes:
call.update(strike=k)
call_values.append(call.present_value())
call.update(strike=orig_strike)
The results visualized.
plt.figure(figsize=(10, 6));
plt.plot(strikes, call_values);
plt.xlabel('strike'); plt.ylabel('call value')
<matplotlib.text.Text at 0x7fd62c271150>
We now take the calibration data and derive/re-calculate values for the option over the first quarter of 2014.
%%time
values = []
for i in range(len(para)):
initial_value, kappa, theta, sigma = para.ix[i][
['initial_value', 'kappa', 'theta', 'sigma']]
vstoxx.update(initial_value=initial_value, kappa=kappa,
theta=theta, volatility=sigma)
values.append(call.present_value())
CPU times: user 7.85 s, sys: 1.52 s, total: 9.37 s Wall time: 9.32 s
The result is a time series with the call option values.
plt.figure(figsize=(10, 6));
plt.plot(para.index, values);
plt.ylabel('call value');
plt.gcf().autofmt_xdate();
Next, and maybe a bit more interesting, we do the same with the data that the multivariate VAR analysis has generated as a forecast for April 2014.
%%time
values = []
for i in range(len(fc)):
initial_value, kappa, theta, sigma = fc.ix[i][
['initial_value', 'kappa', 'theta', 'sigma']]
vstoxx.update(initial_value=initial_value, kappa=kappa,
theta=theta, volatility=sigma)
values.append(call.present_value())
fc['value'] = values
CPU times: user 2.44 s, sys: 476 ms, total: 2.92 s Wall time: 2.85 s
The European call values based on the parameter forecasts visualized.
fc.plot(figsize=(10, 10), subplots=True, color='b');
Summary¶
Some major insights from today:
- Python: Python is good at processing data, i.e. for data logistics
- Python & R: Python and R can easily interact with each other, exchanging data back and forth
- R: R provides powerful statistical libraries that might not be avalilable in Python
- VAR: multivariate vector auto regression can be efficiently and productively applied via the
varspackage (constant + trend + seasonality) - DX: DX Analytics is a Python library for advanced derivatives and risk analytics
- VAR + DX: we have combined mVAR with DX to generate forecasts of derivatives prices given a history of model parameters

http://tpq.io | @dyjh | team@tpq.io
Python Quant Platform | http://quant-platform.com
Python for Finance | Python for Finance @ O'Reilly
Derivatives Analytics with Python | Derivatives Analytics @ Wiley Finance
Listed Volatility and Variance Derivatives | Listed VV Derivatives @ Wiley Finance