The Python Quants

Python and the Financial Community

A Subjective and Biased Overview

Dr. Yves J. Hilpisch

The Python Quants GmbH

analytics@pythonquants.com

www.pythonquants.com

The Python Language

Black-Scholes-Merton (1973) SDE of geometric Brownian motion.

$$ dS_t = rS_tdt + \sigma S_t dZ_t $$

Monte Carlo simulation: draw $I$ standard normally distributed random number $z_t^i$ and apply them to the following by Euler disctretization scheme to simulate $I$ end values of the GBM:

$$ S_{T} = S_0 \exp \left(\left( r - \frac{1}{2} \sigma^2\right) T + \sigma \sqrt{T} z_T \right) $$

Latex description of Euler discretization.

S_T = S_0 \exp (( r - 0.5 \sigma^2 ) T + \sigma \sqrt{T} z_T)

Python implementation of algorithm.

In [1]: 
from pylab import *
S0 = 100.; r = 0.01; T = 0.5; sigma = 0.2
ST = S0 * exp((r - 0.5 * sigma ** 2) * T
     + sigma * sqrt(T) * standard_normal(10000))

Interactive visualization of simulation results.

In [2]: 
%matplotlib inline
hist(ST, bins=40);
grid(True)

The Python Ecosystem

  • IPython (Notebook)
  • NumPy (fast, vectorized array operations)
  • SciPy (collection of scientific classes/functions)
  • pandas (times series and tabular data)
  • PyTables (hardware-bound IO operations)
  • scikit-learn (machine learning algorithms)
  • statsmodels (statistical classes/functions)
  • xlwings (Python-Excel integration)

Financial Libraries

By others:

  • zipline (backtesting of trading algos)
  • matplotlib.finance (financial plots)
  • Python wrappers (QuantLib)

By us:

  • DEXISION – GUI-based financial engineering
  • DX Analytics – global valuation of multi-risk derivatives and portfolios

APIs

  • OANDA (fx trading platform)
  • Thomson Reuters (wrapper for unified API in the making)
  • ...

Integration

  • C/C++ (natively)
  • Julia (IPython)
  • JavaScript (IPython)
  • R (IPython/rpy2)
  • Matlab (NumPy)
  • ...

Pushing data from Python to R.

In [3]: 
%load_ext rpy2.ipython
In [4]: 
X = arange(100)
Y = 2 * X + 5 + 2 * standard_normal(len(X))
%Rpush X Y

Generating plots with R.

In [5]: 
%R plot(X, Y, pch=19, col='blue'); grid(); title("R Plot with IPython")

Doing statistics in R.

In [6]: 
%R print(summary(lm(Y~X)))


Call:
lm(formula = Y ~ X)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.6160 -1.3221  0.0707  1.2701  5.5099 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 4.973043   0.415827   11.96   <2e-16 ***
X           2.000921   0.007257  275.73   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.095 on 98 degrees of freedom
Multiple R-squared:  0.9987,	Adjusted R-squared:  0.9987 
F-statistic: 7.603e+04 on 1 and 98 DF,  p-value: < 2.2e-16

Pulling data from R to Python.

In [7]: 
%R c = coef(lm(Y~X))
%Rpull c
c
Out[7]:
<FloatVector - Python:0x10b211b90 / R:0x1017576a8>
[4.973043, 2.000921]

Performance

Finance algorithms are loop-heavy; Python loops are slow; Python is too slow for finance.

In [8]: 
def counting_py(N):
    s = 0
    for i in xrange(N):
        for j in xrange(N):
            s += int(cos(log(1)))
    return s
In [9]: 
N = 2000
%time counting_py(N)
# memory efficient but slow

CPU times: user 19 s, sys: 18.7 ms, total: 19.1 s
Wall time: 19.1 s
Out[9]:
4000000

First approach: vectorization with NumPy.

In [10]: 
%%time
arr = ones((N, N))
print int(sum(cos(log(arr))))
# much faster but NOT memory efficient

4000000
CPU times: user 96.6 ms, sys: 54.9 ms, total: 151 ms
Wall time: 153 ms
In [11]: 
arr.nbytes
Out[11]:
32000000

Second approach: dynamic compiling with Numba.

In [12]: 
import numba
counting_nb = numba.jit(counting_py)
In [13]: 
%time counting_nb(N)

CPU times: user 152 ms, sys: 23.6 ms, total: 176 ms
Wall time: 220 ms
Out[13]:
4000000
In [14]: 
%timeit counting_nb(N)
# even faster AND memory efficient

10 loops, best of 3: 54.5 ms per loop

Hardware-bound IO operations are standard for Python.

In [15]: 
arr = standard_normal((12500, 10000))
arr.nbytes
# a giga byte worth of data
Out[15]:
1000000000
In [16]: 
%time save('data', arr)

CPU times: user 55.1 ms, sys: 1.85 s, total: 1.91 s
Wall time: 2.35 s
In [17]: 
!ls -n data*

-rw-r--r--  1 501  20  1000000080 22 Sep 16:14 data.npy
In [18]: 
!rm data*

Python Quant Platform

Integrating it all and adding collaboration and scalability (http://quant-platform.com).

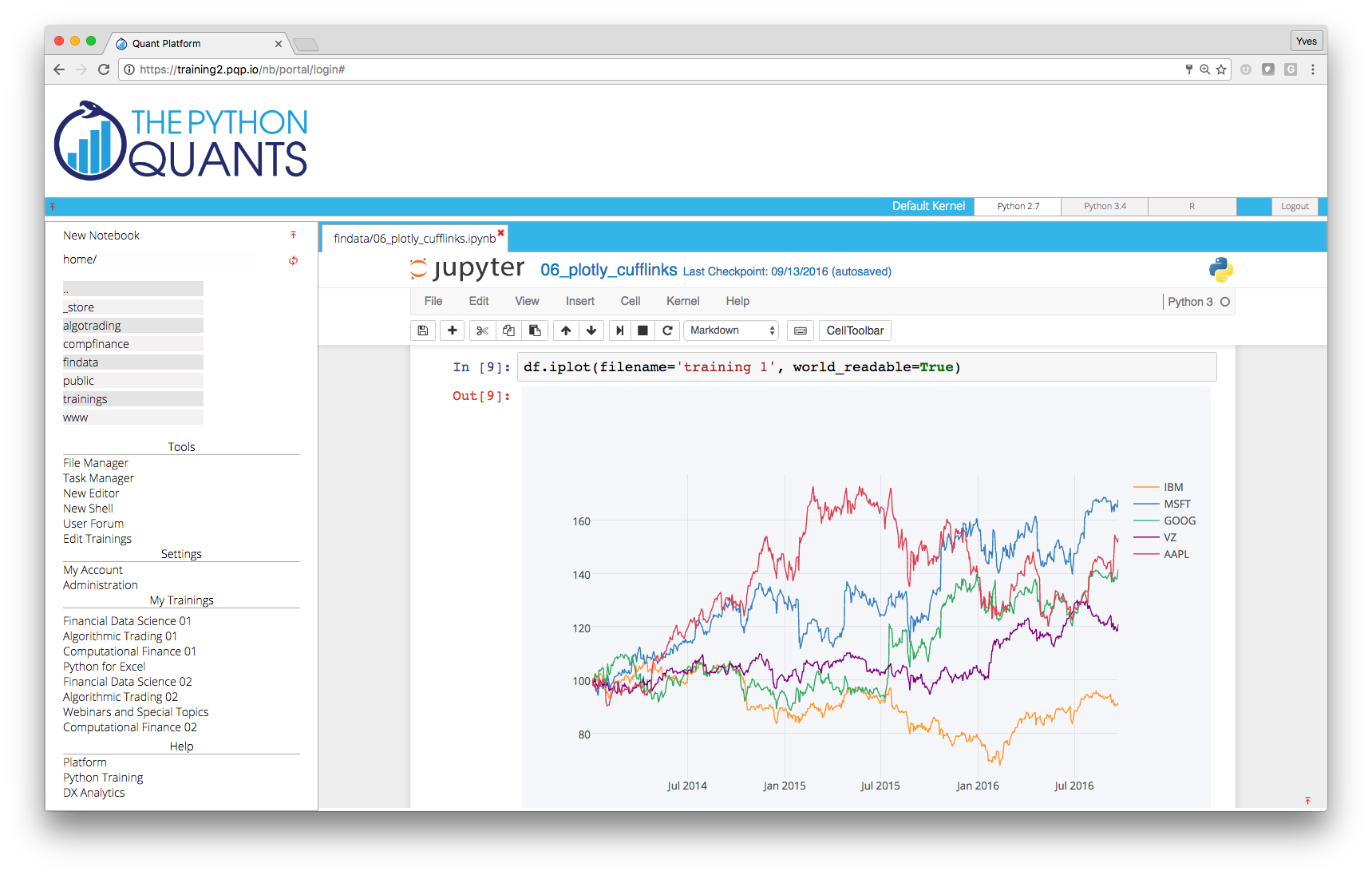
The Large Banks

  • Bank of America Merill Lynch (Quartz platform)
  • JPMorgan Chase (Athena platform)
  • ...

The Hedge Funds

  • AQR Capital Management (origin of pandas)
  • Two Sigma Investments (large scale data analytics)
  • ARC Investments (full-fledged Python for vol trading)
  • ...

Innovators in the Space

  • Quantopian (algo trading & backtesting)
  • Washington Square Technologies (trade & risk platform)
  • Deutsche Boerse/Eurex (VSTOXX and Variance Advanced Services)
  • ...

Python-based tutorials by Eurex (http://www.eurexchange.com/vstoxx/).

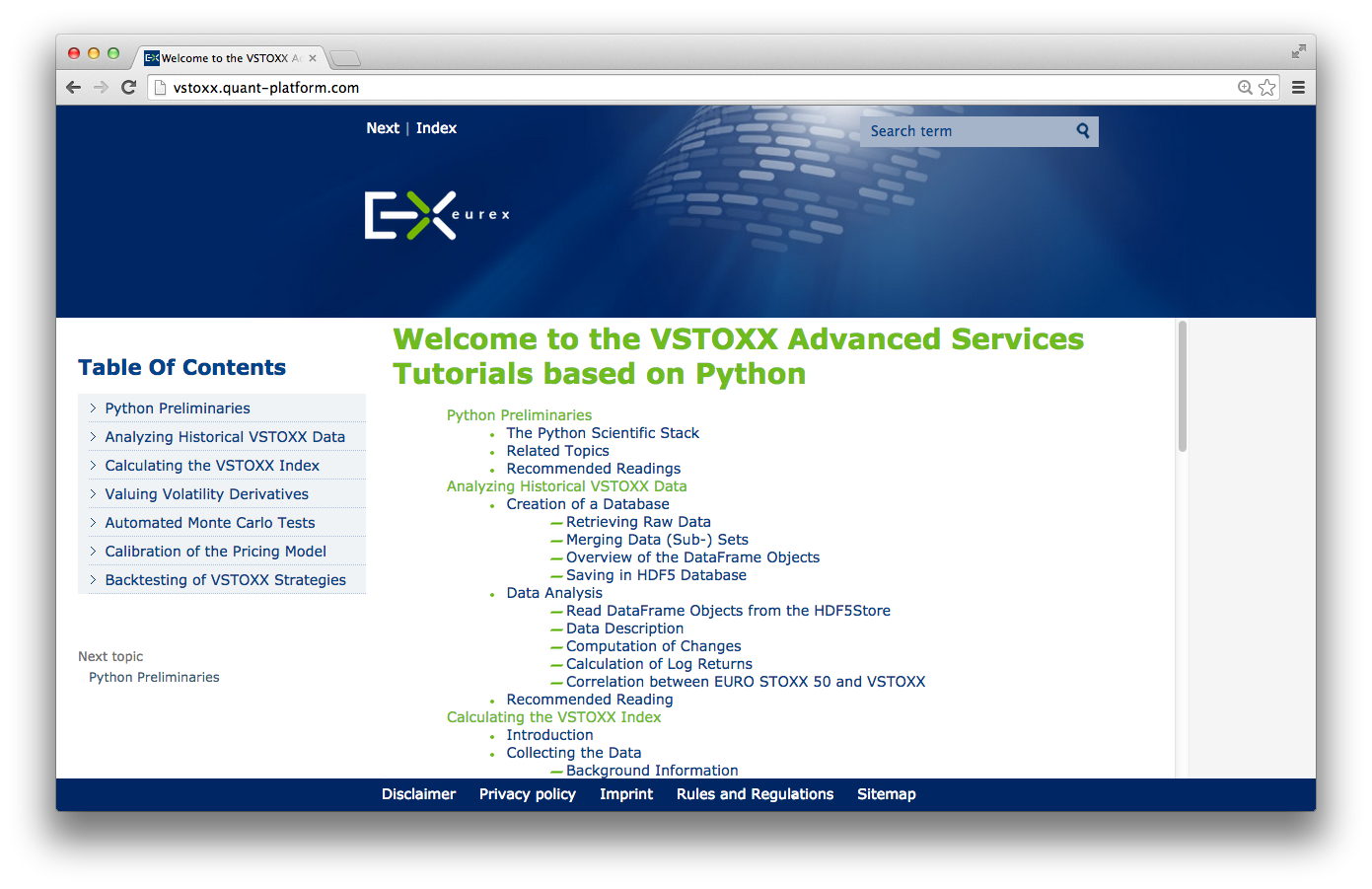
Books

By others:

  • Python for Financial Modelling @ Wiley Finance (2009)
  • Python for Finance @ Packt Publishing (2014)

By myself:

  • Python for Finance – Analyze Big Financial Data @ O'Reilly (2014)
  • Derivatives Analytics with Python @ Wiley Finance (2015)

Integrated offering: book + notebooks + platform + training + ...

Financial Research

"The appendices present an implementation in Python of our experiments." (p. 3)

Education

  • Master of Financial Engineering @ Baruch College CUNY
  • Master of Data Science @ City University of New York
  • Numerical Option Pricing with Python @ Saarland University
  • ...

Baruch College Web site:

"Knowledge and Skills: Our graduates have working experience with C++, VBA, Python, R, and Matlab for financial applications. They share an exceptionally strong work ethic and possess excellent interpersonal, teamwork, and communication skills."

Training

By others:

  • Python for Finance @ Continuum Analytics
  • Python for Finance @ Enthought

By myself:

  • Python for Quant Finance @ Python for Quant Finance Meetup Group
  • Python for Finance @ http://quantshub.com
  • NumPy & pandas for Finance @ CQF Institute/Fitch Learnings
  • ...

Meetups

For Python Quants Conference

  • 1st conference in New York City on 14. March 2014
  • 2nd conference in London on 28. November 2014
  • 3rd conference planned for QI 2015 in Asia (eg Shanghai)

http://forpythonquants.com

Contact us

Please contact us if you have any questions or want to get involved in our Python community events.

The Python Quants

www.pythonquants.com | @dyjh

analytics@pythonquants.com

Python Quant Platform | http://quant-platform.com

Derivatives Analytics with Python | Derivatives Analytics @ Wiley Finance

Python for Finance | Python for Finance @ O'Reilly