The Python Quants

A Better Future with Python

Dr. Yves J. Hilpisch

The Python Quants GmbH

www.pythonquants.com

yves@pythonquants.com

@dyjh

EuroPython, Florence, 03. July 2013

Better Future

Progress

How can economic and/or social progress be measured?

Efficiency – use less resources for a given output
Productivity – generate more output from given resources
Quality – create something new

Language

"It is argued that language plays an active role in the development of scientific ideas. ...

And is mathematics somehow more or less than a language? ...

A particular characteristic of mathematics which appears in one aspect to differentiate it from language is its appeal to visual thinking."

Alan Ford and F. David Peat (1988): "The Role of Language in Science."

"As I gradually improved my in-code documentation, I realized that English is a natural language, but computer languages, regardless of how well we use them, are still 'code.' Communication via natural language is a relatively quick and efficient process. Not so with computer languages: They must be 'decoded' for efficient human understanding."

David Zokaities (2004): "Writing Understandable Code".

Today's trinity of scientifc languages:

the spoken/written language – in general English
the formal language – logic, mathematics, etc.
the programming language – Python, for example

Python seems to be the natural completion of the scientific language stack:

English

"Calculate the inner values of an option at maturity with strike of 105 for 10,000 simulated prices of stock S."

Mathematics

$$ S_0 = 100 $$ $$ K = 105 $$ $$ I = 10000 $$ $$ S_T^i \in \{S_T^1, ... , S_T^I\} $$ $$ h_T^i = \max(S_T^i - K, 0) $$

Python/NumPy

In [1]:

S0 =100
K = 105
I = 10000
ST = S0 * standard_normal(I)
h = maximum(ST - K, 0)

Scientific publishing has been revolutionized by Latex and its derivatives through combining

word processing with
mathematical formula rendering capabilities

The researcher can by herself/himself generate publication-ready output in a highly customizable fashion.

Then, when the need came up,

syntax highlighting capabilities were added (e.g. for Python)

Nowadays, the tools available in the Python space take all this one step further.

Sphinx
IPython Notebook
PythonTEX

What exactly does this mean?

Executable Code as part of the document sources for automatic inclusion of the code's results.
Open Research with reproducable results for everyone interested.
Higher Efficiency, Productivity, Quality

In [2]:

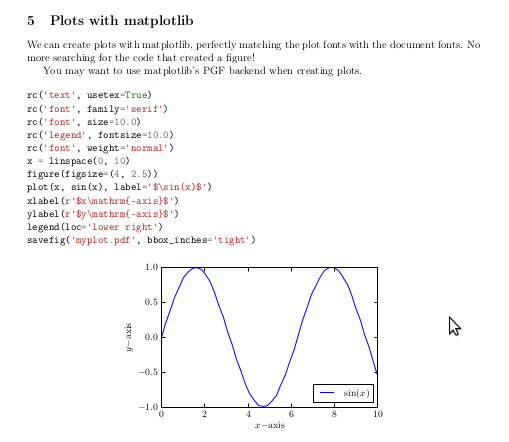
#  \section{Plots with matplotlib}

#  We can create plots with matplotlib, perfectly matching the plot fonts with the document fonts.
#  No more searching for the code that created a figure!

#  You may want to use matplotlib's PGF backend when creating plots.

#  \begin{pylabblock}
#  rc('text', usetex=True)
#  rc('font', family='serif')
#  rc('font', size=10.0)
#  rc('legend', fontsize=10.0)
#  rc('font', weight='normal')
#  x = linspace(0, 10)
#  figure(figsize=(4, 2.5))
#  plot(x, sin(x), label='$\sin(x)$')
#  xlabel(r'$x\mathrm{-axis}$')
#  ylabel(r'$y\mathrm{-axis}$')
#  legend(loc='lower right')
#  savefig('myplot.pdf', bbox_inches='tight')
#  \end{pylabblock}

#  \begin{center}
#  \includegraphics{myplot}
#  \end{center}

Source www.github.com.

PythonTEX

Source www.github.com.

Efficiency

To reach a given goal with minimal resources.

Genome Sequencing

Using Python to generate faster research results.

"Saturday, June 22, 2013

Python for Next-Generation Sequencing

... a story about how a challenging genome sequencing project demonstrated once again, what an awesome tool Python can be ...

Here are the results from one million regular expression searches of a genome of 250 million bases:

Number of matches found in sequence = 61,226
1,000,000 searches completed in 0.671034 seconds
Mean search time = 6.71034e-07 seconds

Fast! ...

Like much of the Python Standard Library, the re module that handles regular expressions is actually written in C, so while the initial function call to the search may be handled by the Python interpreter, the subsequent search is actually being run in compiled native code, which explains its efficiency."

Source www.digitalbiologist.com.

Just-in-Time Compiling

Reducing execution time.

Let's start with pure Python.

In [3]:

def f(m, n):
    total = 0.0
    for i in range(m):
        for j in range (n):
            total += sin(i * j)
    return total

In [4]:

m = 1000
n = m
%time f(m, n)

CPU times: user 3.17 s, sys: 0 ns, total: 3.17 s
Wall time: 3.11 s

Out[4]:

72.546940595631213

The compiled version.

In [5]:

import numba
f_jit = numba.autojit(f)

In [6]:

%time f_jit(n, m)

CPU times: user 181 ms, sys: 14 ms, total: 195 ms
Wall time: 213 ms

Out[6]:

72.54694059563121

The NumPy solution.

In [7]:

def f_np(m, n):
    v1 = resize(arange(m), (n, m))
    v2 = resize(arange(n), (m, n))
    v = v1 * v2.T
    return m * n, sum(sin(v))

In [8]:

%time f_np(m, n)

CPU times: user 71 ms, sys: 43 ms, total: 114 ms
Wall time: 114 ms

Out[8]:

(1000000, 72.546940595631213)

Wait a minute: Although the NumPy solution is faster, what about memory issues with "too large" arrays?

NumPy solution will break down.
Numba solution will still work.

Future: Blaze – disk-based, possibly distributed, arrays for big data (think of a combination of NumPy and PyTables on steroids)

Productivity

To generate maximum output given your resources.

Parallel Execution of Code

Increasing the output given a certain algorithm and hardware.

The algorithm we (arbitrarily) choose is the Monte Carlo estimator for a European option in the Black-Scholes-Merton set-up.

$$dS_t = r S_t dt + \sigma S_t dZ_t$$

In [9]:

def BSM_MCS(S0):
    ''' Black-Scholes-Merton MCS Estimator for European Calls. '''
    import numpy as np
    K = 100.; T = 1.0; r = 0.05; vola = 0.2
    M = 50; I = 20000
    dt = T / M
    rand = np.random.standard_normal((M + 1, I))
    S = np.zeros((M + 1, I)); S[0] = S0
    for t in range(1, M + 1):
        S[t] = S[t-1] * np.exp((r - 0.5 * vola ** 2) * dt + vola * np.sqrt(dt) * rand[t])
    BSM_MCS_Value = np.sum(np.maximum(S[-1] - K, 0)) / I
    return BSM_MCS_Value

The benchmark case of sequential execution.

In [10]:

from time import time
n = 100
def seqValue():
    optionValues = []
    for S in linspace(80, 100, n):
        optionValues.append(BSM_MCS(S))
    return optionValues
t0 = time()
seqValue()
t1 = time(); d1 = t1 - t0
print "Number of Options   %8d" % n
print "Duration in Seconds %8.3f" % d1
print "Options per Second  %8.3f" % (n / d1)

Number of Options        100
Duration in Seconds   14.142
Options per Second     7.071

We initialize the parallel execution infrastructure.

In [11]:

# shell: ipcluster start -n 2
from IPython.parallel import Client
cluster_profile = "default"
c = Client(profile=cluster_profile)
view = c.load_balanced_view()

The function for the parallel execution of a number of different options valuations.

In [12]:

def parValue():
    optionValues = []
    for S in linspace(80, 100, n):
        value = view.apply_async(BSM_MCS, S)
        # asynchronously calculate the option values
        optionValues.append(value)
    return optionValues

The case of parallel execution.

In [13]:

def execution():
    optionValues = parValue()  # calculate all values
    print "Submitted tasks     %8d" % len(optionValues)
    c.wait(optionValues)
    return optionValues
t0 = time()
optionValues = execution()
t1 = time(); d2 = t1 - t0
print "Duration in Seconds %8.3f" % d2
print "Options per Second  %8.3f" % (n / d2)

Submitted tasks          100
Duration in Seconds    7.681
Options per Second    13.019

Interactive Financial Analysis

Maximizing an analyst's output given his daily (weekly, monthly) capacity.

Daily Stock Price Data

Reading and analyzing daily stock price data.

In [14]:

import pandas as pd
import pandas.io.data as pdd

In [15]:

AAPL = pdd.DataReader('AAPL', data_source='yahoo', start='1/1/2003')
# retrieve Apple stock prices from Yahoo Finance since 2003
AAPL['60d'] = pd.rolling_mean(AAPL['Close'], window=60)

In [16]:

AAPL[['Close', '60d']].plot(grid=True)

Out[16]:

<matplotlib.axes.AxesSubplot at 0x4647d50>

High-Frequency Stock Price Data

Reading intraday, high-frequency data from a Web source, resampling and plotting it.

In [17]:

url = 'http://hopey.netfonds.no/posdump.php?date=20130701&paper=AAPL.O&csv_format=csv'
AAPL = pd.read_csv(url, index_col=0, header=0, parse_dates=True)

In [18]:

AAPL

Out[18]:

<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 14894 entries, 2013-07-01 10:00:01 to 2013-07-01 22:20:56
Data columns (total 6 columns):
bid                  14894  non-null values
bid_depth            14894  non-null values
bid_depth_total      14894  non-null values
offer                14894  non-null values
offer_depth          14894  non-null values
offer_depth_total    14894  non-null values
dtypes: float64(2), int64(4)

In [19]:

AAPL_10min = AAPL.resample(rule='10min', how='mean')

In [20]:

AAPL_10min['bid'].plot()

Out[20]:

<matplotlib.axes.AxesSubplot at 0x480fb50>

Quality

Doing new things.

Better Investment Decisions through Regulation

Using Python to making contractual features of ABS transparent.

To increase the ability of investors to assess the quality and mechanisms behind Asset Backed Sercurities (ABS) – those responsible for the financial crisis of 2007/2008 – the Securities and Exchange Commission (SEC) proposed in 2010 to use Python Programs (with XML files) to exactly describe their contractual Flow of Funds ("waterfall").

“We are proposing to require that most ABS issuers file a computer program that gives effect to the flow of funds, or 'waterfall,' provisions of the transaction. We are proposing that the computer program be filed on EDGAR in the form of downloadable source code in Python. Python, as we will discuss further below, is an open source interpreted programming language. Under our proposal, an investor would be able to download the source code for the waterfall computer program and run the program on the investor’s own computer (properly configured with a Python interpreter). The waterfall computer program would be required to allow use of the asset data files that we are also proposing today. This proposed requirement is designed to make it easier for an investor to conduct a thorough investment analysis of the ABS offering at the time of its initial investment decision.”

Source SEC Proposal (2010), pp. 205-206.

Analyzing and Explaining the Universe

Using Python for Cosmological and Open Research

Local Group Kinematics Arxiv

Source www.arxiv.org.

Local Group Kinematics Github

Source www.github.com.

Local Group Kinematics IPYNB

Source www.github.com.

Value Added Services with Python

Using Python to communicate financial theory and derivative product features.

Eurex, one of the leading derivatives exchanges, recently launched a new Python-based marketing initiative called VSTOXX® Advanced Services.

"VSTOXX® Advanced Services

Benefits for professional trading. Free!

Futures and options on the VSTOXX® give investors and traders a targeted and leveraged means to take a view on European volatility, based on the implied volatility derived from EURO STOXX 50® Index Options. Portfolio diversification and optimizing volatility exposure are amongst the strongest reasons to access volatility via VSTOXX® derivatives.

Our advanced VSTOXX® Services offer a number of added benefits for professional trading. On the following pages you will find a wealth of information – tutorials, scripts and tools for back testing – that help you efficiently analyze data related to the VSTOXX® volatility index, understand how the VSTOXX® volatility index is calculated and how you can value derivatives written on the VSTOXX® index."

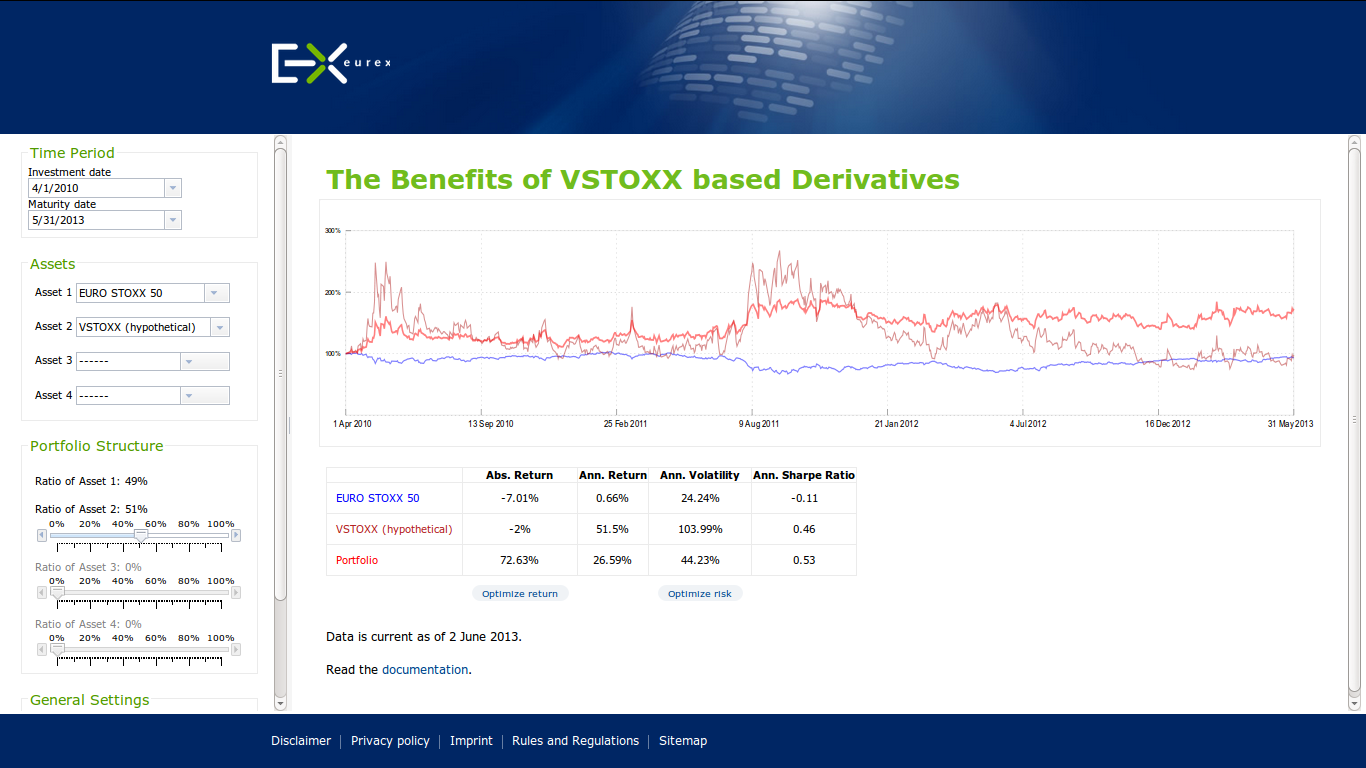
Source www.eurexchange.com.

The VSTOXX® Advanced Services do

provide an educational one-stop offering regarding the VSTOXX® and related derivatives
provide the necessary theoretical background in a concise yet complete fashion
provide Python scripts that are self-contained, illustrate the theoretical concepts and that are immediately applicable

In economic terms, the project obviously shall facilitate trading in the respective products to increase liquidity. This should be mainly reached by lowering barriers of entry to this cutting edge product class.

The main tool used is "applicable transparency" through providing executable Python scripts.

Major target groups are:

traders
investors
risk managers
quants
developers
researchers
teachers/students

Why Python?

Open Source
Concise "Mathematical" Syntax
Financial Features
General Purpose Language
Long-Term Strategic View

Which libraries & tools?

NumPy
pandas
SciPy
matplotlib
PyTables
Sphinx

... the standard scientific stack.

Web-based, Collaborative Data Analytics

... and Development, Visualization, Presentation, Publication, Documentation

Wakari

Source www.wakari.io.

Maybe Our Biggest Challenge ...

... to make the use of Python as simple and reliable as possible

As a community, we should put our emphasis, among others, maybe even more on topics like:

Education – at schools, universities, in trainings, through books
Installation – distribution (e.g. Anaconda), Web services (e.g. Wakari.io), packaging (e.g. Binstar.org)
Standardization – language (2 vs. 3), style (PEP 8), documentation (Sphinx)
Building Services – professionally supporting libraries, packages, distributions

The Python Quants

The Python Quants GmbH – Experts for Python in Quant Finance

The Python Quants GmbH – the company Web site

www.pythonquants.com

Dr. Yves J. Hilpisch – my personal Web site

www.hilpisch.com

Derivatives Analytics with Python – my new book

Read an Excerpt and Order the Book

Contact Us

yves@pythonquants.com

@dyjh