Browser-based, Collaborative Financial & Derivatives Analytics¶
Python Quant Platform and DX Analytics
Dr. Yves J. Hilpisch | The Python Quants GmbH
analytics@pythonquants.com | www.pythonquants.com
For Python Quants Conference, 28. November 2014
The Python Language¶
Black-Scholes-Merton (1973) SDE of geometric Brownian motion. The "Hello World example of Quant Finance."
$$ dS_t = rS_tdt + \sigma S_t dZ_t $$
Monte Carlo simulation: draw $I$ standard normally distributed random number $z_t^i$ and apply them to the following by Euler disctretization scheme to simulate $I$ end values of the GBM:
$$ S_{T} = S_0 \exp \left(\left( r - \frac{1}{2} \sigma^2\right) T + \sigma \sqrt{T} z_T \right) $$
Latex description of Euler discretization.
S_T = S_0 \exp (( r - 0.5 \sigma^2 ) T + \sigma \sqrt{T} z_T)
Python implementation of algorithm.
from pylab import *
S_0 = 100.; r = 0.01; T = 0.5; sigma = 0.2
z_T = standard_normal(10000)
S_T = S_0 * exp((r - 0.5 * sigma ** 2) * T + sigma * sqrt(T) * z_T)
Again, Latex for comparison:
S_T = S_0 \exp (( r - 0.5 \sigma^2 ) T + \sigma \sqrt{T} z_T)
Interactive visualization of simulation results.
%matplotlib inline
pyfig = figure()
hist(S_T, bins=40);
grid()
The Python Ecosystem¶
The Python ecosystem can be considered one of the major competitive advantages of the language.
- IPython (Notebook)
- NumPy (fast, vectorized array operations)
- SciPy (collection of scientific classes/functions)
- pandas (times series and tabular data)
- PyTables (hardware-bound IO operations)
- scikit-learn (machine learning algorithms)
- statsmodels (statistical classes/functions)
- xlwings (Python-Excel integration)
Integration – No "Either Or" with Python
Python integrates pretty well with almost any other language used for scientific and financial computing.
- C/C++ (natively)
- Julia (IPython)
- JavaScript (IPython)
- R (IPython/rpy2)
- Matlab (NumPy)
- ...
Example: Statistics with R¶
We analyze the statistical correlation between the EURO STOXX 50 stock index and the VSTOXX volatility index.
First, reading the EURO STOXX 50 & VSTOXX data.
import pandas as pd
es = pd.HDFStore('data/SX5E.h5', 'r')['SX5E']
vs = pd.HDFStore('data/V2TX.h5', 'r')['V2TX']
es['SX5E'].plot(figsize=(9, 6))
<matplotlib.axes.AxesSubplot at 0x10f9d5f10>
Generating log returns with Python and pandas.
import numpy as np
# log returns for the major indices' time series data
datv = pd.DataFrame({'SX5E' : es['SX5E'], 'V2TX': vs['V2TX']}).dropna()
rets = np.log(datv / datv.shift(1)).dropna()
ES = rets['SX5E'].values
VS = rets['V2TX'].values
Bridging to R from within IPython Notebook and pushing Python data to the R run-time.
%load_ext rpy2.ipython
The rpy2.ipython extension is already loaded. To reload it, use: %reload_ext rpy2.ipython
%Rpush ES VS
Plotting with R in IPython Notebook.
%R plot(ES, VS, pch=19, col='blue'); grid(); title("Log returns ES50 & VSTOXX")
Linear regression with R.
%R c = coef(lm(VS~ES))
<FloatVector - Python:0x115c647e8 / R:0x10bd931c8> [-0.000074, -2.752754]
%R print(summary(lm(VS~ES)))
Call:
lm(formula = VS ~ ES)
Residuals:
Min 1Q Median 3Q Max
-0.32412 -0.02188 -0.00213 0.02015 0.53675
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -7.416e-05 6.169e-04 -0.12 0.904
ES -2.753e+00 4.078e-02 -67.50 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.03905 on 4006 degrees of freedom
Multiple R-squared: 0.5321, Adjusted R-squared: 0.532
F-statistic: 4556 on 1 and 4006 DF, p-value: < 2.2e-16
Regression line visualized.
%R plot(ES, VS, pch=19, col='blue'); grid(); abline(c, col='red', lwd=5)
Pulling data from R to Python and using it.
%Rpull c
plt.figure(figsize=(9, 6))
plt.plot(ES, VS, 'b.')
plt.plot(ES, c[0] + c[1] * ES, 'r', lw=3)
plt.grid(); plt.xlabel('ES'); plt.ylabel('VS')
<matplotlib.text.Text at 0x116005690>
If you want to have it nicer, interactive and embeddable anywhere – use plot.ly
import plotly.plotly as ply
ply.sign_in('yves', 'token')
Let us generate a plot with fewer data points.
pyfig = plt.figure(figsize=(9, 6)); n = 100
plt.plot(ES[:n], VS[:n], 'b.')
plt.plot(ES[:n], c[0] + c[1] * ES[:n], 'r', lw=3)
plt.grid(); plt.xlabel('ES'); plt.ylabel('VS')
<matplotlib.text.Text at 0x11623f510>
Only single line of code needed to convert matplotlib plot into interactive D3 plot.
ply.iplot_mpl(pyfig) # convert mpl plot into interactive D3
Example: Working with Julia¶
Julia is, for example, often faster for recursive function formulations. As an example, consider the Fibonacci sequence.
# quite slow in Python
def fib_rec(n):
if n < 2:
return n
else:
return fib_rec(n - 1) + fib_rec(n - 2)
%time fib_rec(35)
CPU times: user 2.87 s, sys: 29 ms, total: 2.9 s Wall time: 2.85 s
9227465
%%julia
# much faster in Julia
fib_rec(n) = n < 2 ? n : fib_rec(n - 1) + fib_rec(n - 2)
@elapsed fib_rec(35)
fib_rec (generic function with 1 method) 0.072275267
For comparison, an iterative function implementation.
# iterative version in Python
def fib_it(n):
x,y = 0, 1
for i in xrange(1, n + 1):
x, y = y, x + y
return x
%time fn = fib_it(1000000) # with 1,000,000
CPU times: user 9.6 s, sys: 32 ms, total: 9.64 s Wall time: 9.41 s
%%julia
# iterative version in Julia
function fib_it(n)
x, y = (0,1)
for i = 1:n
x, y = (y, x + y)
end
return x
end
fib_it(5) # initial call
@elapsed fib_it(10000000) # with 10,000,000
fib_it (generic function with 1 method) 5 0.005006169
For final comparison, the dynamically compiled Python version with Numba.
import numba
fib_nb = numba.jit(fib_it)
%timeit fib_nb(10000000) # with 10,000,000
100 loops, best of 3: 4.91 ms per loop
Performance – Numerical Algorithms
Finance algorithms are loop-heavy; Python loops are slow; Python is too slow for finance.
def counting_py(N):
s = 0
for i in xrange(N):
for j in xrange(N):
s += int(cos(log(1)))
return s
N = 2000
%time counting_py(N)
# memory efficient but slow
CPU times: user 10.7 s, sys: 782 ms, total: 11.5 s Wall time: 10.9 s
4000000
First approach: vectorization with NumPy.
%%time
arr = ones((N, N))
print int(sum(cos(log(arr))))
4000000 CPU times: user 109 ms, sys: 49.4 ms, total: 158 ms Wall time: 201 ms
arr.nbytes # much faster but NOT memory efficient
32000000
Second approach: dynamic compiling with Numba.
import numba
counting_nb = numba.jit(counting_py)
%time counting_nb(N)
# some overhead the first time
CPU times: user 177 ms, sys: 56.5 ms, total: 234 ms Wall time: 367 ms
4000000
%timeit counting_nb(N)
# even faster AND memory efficient
10 loops, best of 3: 56.7 ms per loop
Performance – Hardware-bound IO
Hardware-bound IO operations are standard for Python.
%time one_gb = standard_normal((12500, 10000))
one_gb.nbytes
# a giga byte worth of data
CPU times: user 5.66 s, sys: 435 ms, total: 6.1 s Wall time: 7.11 s
1000000000
%time save('one_gb', one_gb)
CPU times: user 54.9 ms, sys: 1.77 s, total: 1.82 s Wall time: 2.58 s
!ls -n one_gb*
-rw-r--r-- 1 501 20 1000000080 21 Nov 20:50 one_gb.npy
!rm one_gb*
Python Quant Platform¶
Integrating it all and adding collaboration and scalability (http://quant-platform.com).
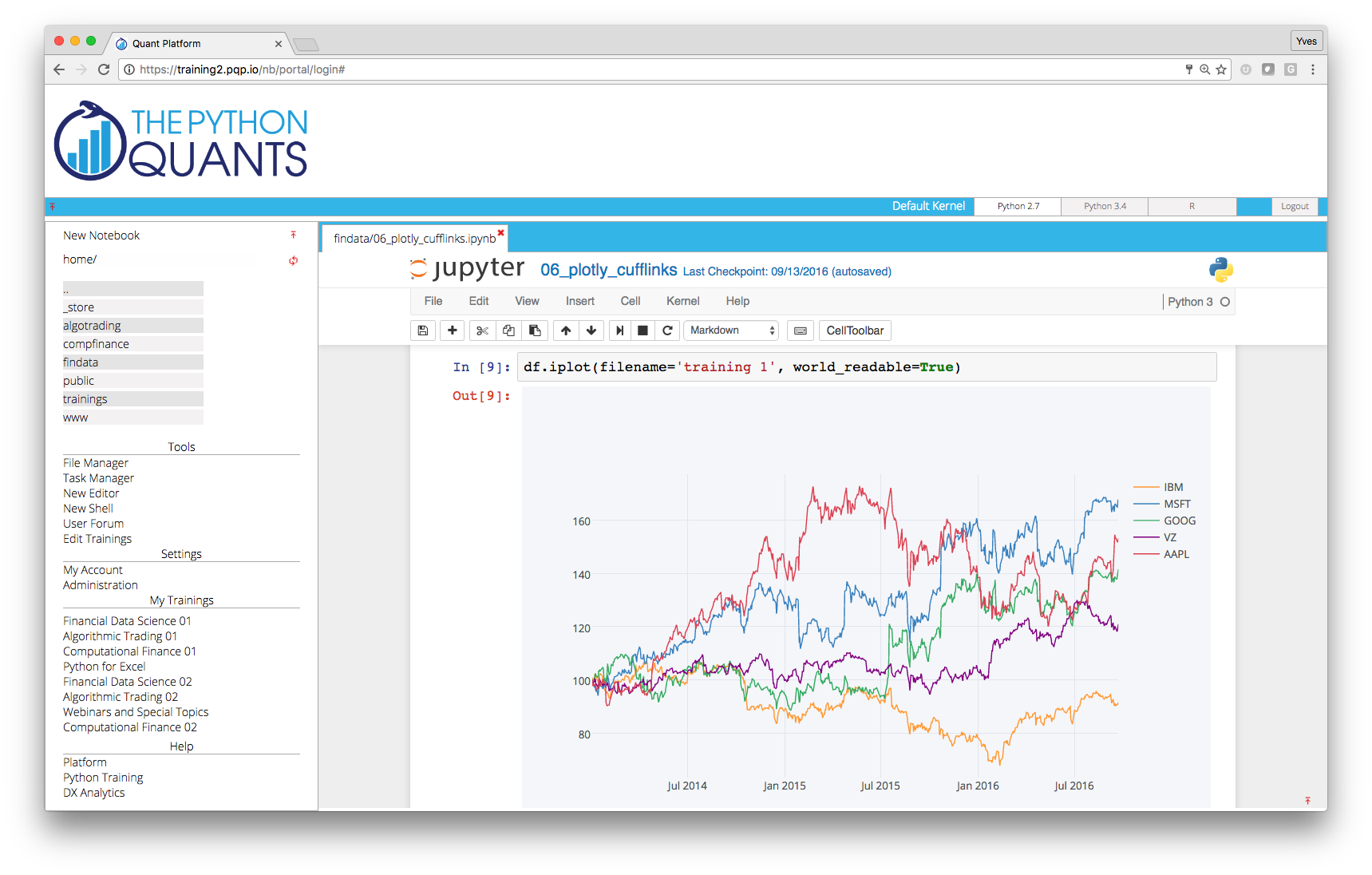
At the moment, the Python Quant Platform comprises the following components and features:
- IPython Notebook: interactive data and financial analytics in the browser with full Python integration and much more (cf. IPython home page).
- IPython Shell, Python Shell, System Shell: all you typically do on the (local or remote) system shell (Vim, Git, file operations, etc.)
- Anaconda Python Distribution: complete Python stack for financial, scientific and data analytics workflows/applications (cf. Anaconda page); you can easily switch between Python 2.7 and 3.4.
- R Stack: for statistical analyses, integrated via
rpy2and IPython Notebook - Julia: the "high-level, high-performance dynamic programming language for technical computing"
- DX Analytics: our library for advanced financial and derivatives analytics with Python based on Monte Carlo simulation.
- File Manager: a GUI-based File Manager to upload, download, copy, remove, rename files on the platform.
- Chat/Forum: there is a simple chat/forum application available via which you can share thoughts, documents and more.
- Collaboration: the platform features user/group administration as well as file sharing via public folders.
- Linux Server: the platform is powered by Linux servers to which you have full shell access.
- Deployment: the platform is easily scalable since it is cloud-based and can also be easily deployed on your own servers (via Docker containers).
During the NumPy workshop on 27. November 2014 at CQF Institute ...

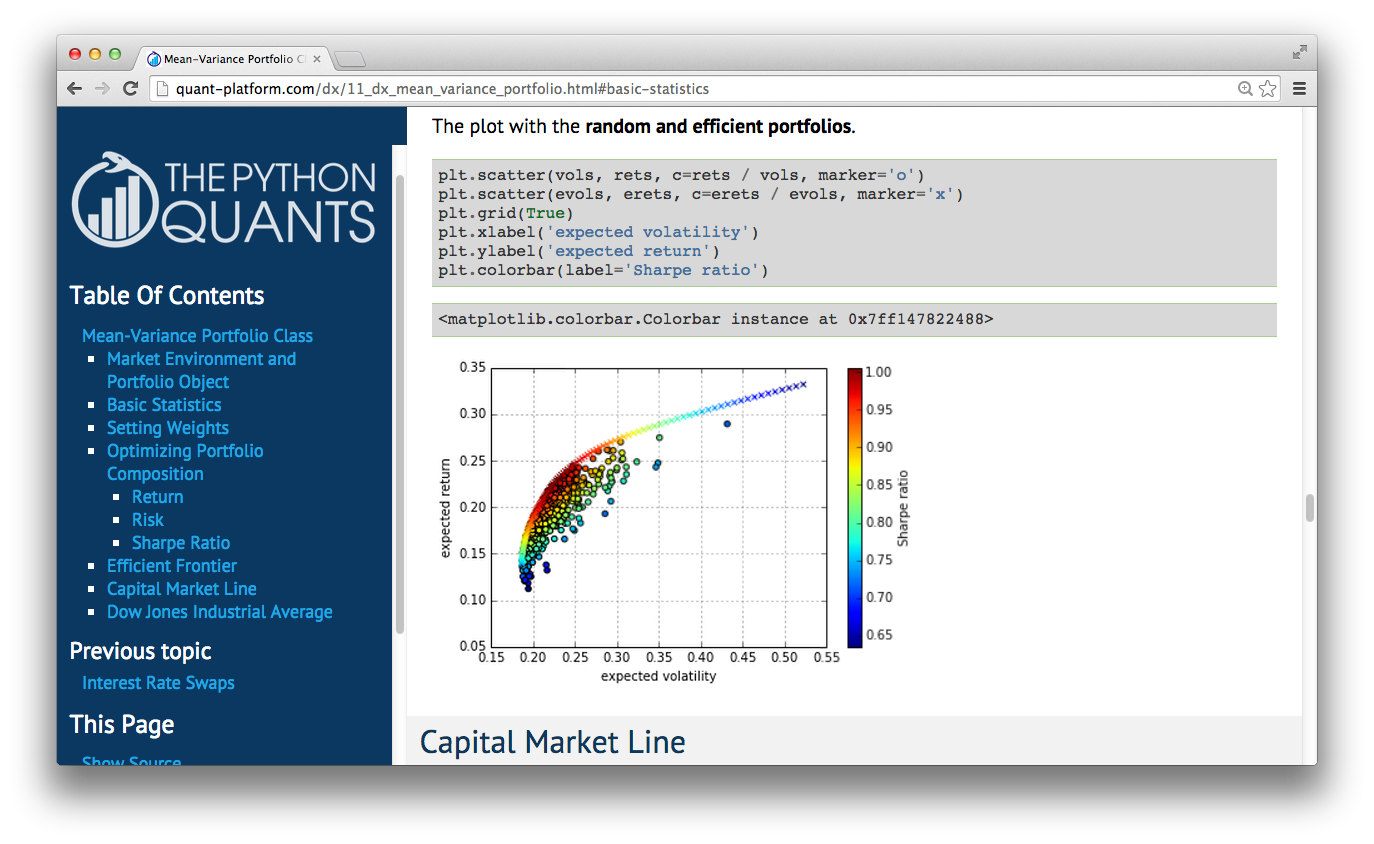
DX Analytics¶
DX Analytics is a Python library for advanced derivatives and risk analytics. Just recently open sourced (cf. http://dx-analytics.com and http://github.com/yhilpisch/dx)
Why DX Analytics? A brief History.¶
Important research milestones (I), from a rather personal perspective.
- Bachelier (1900) – Option Pricing with Arithmetic Brownian Motion
- Einstein (1905) – Rigorous Theory of Brownian Motion
- Samuelson (1950s) – Systematic Approaches to Option Pricing
- Black Scholes Merton (1973) – Geometric Brownian Motion, Analytical Option Pricing Formula
- Merton (1976) – Jump Diffusion, Option Pricing with Jumps
- Boyle (1977) – Monte Carlo for European options
- Cox Ross Rubinstein (1979) – Binomial Option Pricing
Important research milestones (II), from a rather personal perspective.
- Harrison Kreps Pliska (1979/1981) – General Risk-Neutral Valuation, Fundamental Theorem of Asset Pricing
- Cox Ingersoll Ross (1985) – Intertemporal General Equilibrium, Short Rates with Square-Root Diffusion
- Heston (1993) – Stochastic Volatility, Fourier-based Option Pricing
- Bates (1996) – Heston (1993) plus Merton (1976)
- Bakshi Cao Chen (1997) – Bates (1996) plus Cox Ingersoll Ross (1985)
- Carr Madan (1999) – Using Fast Fourier Transforms for Option Pricing
- Longstaff Schwartz (2001) – Monte Carlo for American Options
- Gamba (2003) – Monte Carlo for (Complex) Portfolios of Interdependent Options
DX Analytics leverages the experience of using Python for derivatives analytics since about 10 years.
- Ph.D. research – felt in love with Harrison-Kreps-Pliska general valuation approach
- Visixion (The Python Quants) foundation in 2004 – first steps with Python & Monte Carlo simulation
- DEXISION prototyping from 2007 – using Python to build the first prototype
- DEXISION analytics suite from 2009 until today – using Python and Web technologies to provide analytics as a service
- Derivatives Analytics with Python 2011-2014 – writing a book based on university lectures and Python experience (upcoming at Wiley Finance)
- Python for Finance 2013-2014 – wiriting a book teaching Python for finance (explaining basic DX architecture)
- DX Analytics since QIV 2013 – putting all lessons learned together to write a new, concise Python library
General ideas and approaches:
- general risk-neutral valuation ("Global Valuation")
- Monte Carlo simulation for valuation, Greeks
- Fourier-based formulae for calibration
- arbitrary models for stochastic processes
- single & multi risk derivatives
- free to define payoff functions (Python syntax)
- European and American exercise
- completely implemented in Python
- hardware not a limiting factor
You can register for a PQP trial (incl. DX Analytics) here http://trial.quant-platform.com or clone the Github repo from here http://github.com/yhilpisch/dx.
A Realistic Example with DX Analytics¶
Bringing back office simulation and risk management practices to front office analytics.
The following more realistic example illustrates that you can model, value and risk manage quite complex derivatives portfolios with DX Analytics. The example has the following characteristics:
- portfolio over 2 years
- stochastic short rate for risk-neutral discounting
- 250 risk factors (gbm, jump diffusion, stochastic volatility)
- 1,000 derivatives (call and put options, European and American exercise, random maturites)
- monthly frequency for discretization
- 1,000 paths for simulation
from dx import *
np.random.seed(10000)
%matplotlib inline
Stochastic Short Rates¶
Let us start by defining a stochastic discounting object (based on CIR square-root diffusion process).
mer = market_environment(name='me', pricing_date=dt.datetime(2015, 1, 1))
mer.add_constant('initial_value', 0.005)
mer.add_constant('volatility', 0.1)
mer.add_constant('kappa', 2.0)
mer.add_constant('theta', 0.03)
mer.add_constant('paths', 1000) # dummy
mer.add_constant('frequency', 'M') # dummy
mer.add_constant('starting_date', mer.pricing_date)
mer.add_constant('final_date', dt.datetime(2015, 12, 31)) # dummy
ssr = stochastic_short_rate('ssr', mer)
Some simulated short rate paths visualized.
plt.figure(figsize=(9, 5))
plt.plot(ssr.process.time_grid, ssr.process.get_instrument_values()[:, :10]);
plt.gcf().autofmt_xdate(); plt.grid()
Multiple Risk Factors¶
The example is based on a multiple, correlated risk factors (based on geomtetric Brownian motion, jump diffusion or stachastic volatility models). The basic assumptions.
# market environments
me = market_environment('gbm', dt.datetime(2015, 1, 1))
# geometric Brownian motion
me.add_constant('initial_value', 36.)
me.add_constant('volatility', 0.2)
me.add_constant('currency', 'EUR')
In addition to the input parameters of the geometric Brownian motion, we also need the following for the jump diffusions and stochastic volatility models.
# jump diffusion
me.add_constant('lambda', 0.4)
me.add_constant('mu', -0.4)
me.add_constant('delta', 0.2)
# stochastic volatility
me.add_constant('kappa', 2.0)
me.add_constant('theta', 0.3)
me.add_constant('vol_vol', 0.5)
me.add_constant('rho', -0.5)
For the portfolio valuation we also need a valuation environment.
# valuation environment
val_env = market_environment('val_env', dt.datetime(2015, 1, 1))
val_env.add_constant('paths', 1000)
val_env.add_constant('frequency', 'M')
val_env.add_curve('discount_curve', ssr)
val_env.add_constant('starting_date', dt.datetime(2015, 1, 1))
val_env.add_constant('final_date', dt.datetime(2016, 12, 31))
# add valuation environment to market environments
me.add_environment(val_env)
We generate a large number of risk factors (with some random parameter values).
no = 250
risk_factors = {}
for rf in range(no):
# random model choice
sm = np.random.choice(['gbm', 'jd', 'sv'])
key = '%3d_%s' % (rf + 1, sm)
risk_factors[key] = market_environment(key, me.pricing_date)
risk_factors[key].add_environment(me)
# random initial_value
risk_factors[key].add_constant('initial_value',
np.random.random() * 40. + 20.)
# radnom volatility
risk_factors[key].add_constant('volatility',
np.random.random() * 0.6 + 0.05)
# the simulation model to choose
risk_factors[key].add_constant('model', sm)
Correlations are also randomly chosen.
correlations = []
keys = sorted(risk_factors.keys())
for key in keys[1:]:
correlations.append([keys[0], key, np.random.choice([-0.05, 0.0, 0.05])])
correlations[:3]
[[' 1_jd', ' 2_jd', -0.050000000000000003], [' 1_jd', ' 3_sv', 0.050000000000000003], [' 1_jd', ' 4_sv', -0.050000000000000003]]
Options Modeling¶
We model a certain number of derivative instruments with the following major assumptions.
me_option = market_environment('option', me.pricing_date)
# choose from a set of maturity dates (month ends)
maturities = pd.date_range(start=me.pricing_date,
end=val_env.get_constant('final_date'),
freq='M').to_pydatetime()
me_option.add_constant('maturity', np.random.choice(maturities))
me_option.add_constant('currency', 'EUR')
me_option.add_environment(val_env)
Portfolio Modeling¶
The derivatives_portfolio object we compose consists of a large number derivatives positions. Each option differs with respect to the strike and the risk factor it is dependent on.
positions = {}
for i in range(4 * no):
ot = np.random.choice(['am_put', 'eur_call'])
if ot == 'am_put':
otype = 'American single'
payoff_func = 'np.maximum(%5.3f - instrument_values, 0)'
else:
otype = 'European single'
payoff_func = 'np.maximum(maturity_value - %5.3f, 0)'
# random strike
strike = np.random.randint(36, 40)
underlying = sorted(risk_factors.keys())[(i + no) % no]
positions[i] = derivatives_position(
name='option_pos_%d' % strike,
quantity=np.random.randint(1, 10),
underlyings=[underlying],
mar_env=me_option,
otype=otype,
payoff_func=payoff_func % strike)
# number of derivivatives positions
len(positions)
1000
Portfolio Valuation¶
All is together to define the derivatives portfolio.
port_sequ = derivatives_portfolio(
name='portfolio',
positions=positions,
val_env=val_env,
risk_factors=risk_factors,
correlations=correlations,
parallel=False) # sequential calculation
The correlation matrix illstrates the market complexity.
port_sequ.val_env.get_list('correlation_matrix')
| 1_jd | 2_jd | 3_sv | 4_sv | 5_gbm | 6_gbm | 7_jd | 8_gbm | 9_sv | 10_sv | ... | 241_jd | 242_sv | 243_sv | 244_sv | 245_gbm | 246_jd | 247_jd | 248_sv | 249_sv | 250_jd | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1_jd | 1.00 | -0.05 | 0.05 | -0.05 | -0.05 | 0.05 | -0.05 | -0.05 | 0.05 | 0.05 | ... | -0.05 | 0.05 | 0.05 | -0.05 | 0.05 | 0 | 0.05 | 0.05 | 0 | 0 |
| 2_jd | -0.05 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 3_sv | 0.05 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 4_sv | -0.05 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 5_gbm | -0.05 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 6_gbm | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 7_jd | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 8_gbm | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 9_sv | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 10_sv | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 11_jd | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 12_jd | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 13_jd | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 14_sv | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 15_sv | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 16_jd | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 17_jd | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 18_sv | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 19_sv | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 20_jd | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 21_sv | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 22_gbm | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 23_gbm | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 24_sv | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 25_sv | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 26_jd | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 27_gbm | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 28_gbm | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 29_sv | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 30_sv | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 221_jd | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 222_sv | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 223_gbm | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 224_jd | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 225_jd | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 226_sv | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 227_sv | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 228_jd | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 229_sv | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 230_sv | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 231_gbm | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 232_sv | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 233_gbm | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 234_jd | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 235_gbm | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 236_gbm | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 237_jd | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 238_gbm | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 239_jd | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 240_gbm | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 241_jd | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 242_sv | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 243_sv | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 244_sv | -0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 245_gbm | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0 | 0.00 | 0.00 | 0 | 0 |
| 246_jd | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1 | 0.00 | 0.00 | 0 | 0 |
| 247_jd | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 1.00 | 0.00 | 0 | 0 |
| 248_sv | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 1.00 | 0 | 0 |
| 249_sv | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 1 | 0 |
| 250_jd | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ... | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | 0.00 | 0.00 | 0 | 1 |
250 rows × 250 columns
The call of the get_values method to value all instruments.
%time res = port_sequ.get_statistics(fixed_seed=True)
Totals pos_value 47946.1000 pos_delta 644.2146 pos_vega 44614.5193 dtype: float64 CPU times: user 16min 15s, sys: 1min, total: 17min 15s Wall time: 8min 40s
The resulting table with the results.
res.set_index('position', inplace=False)
| name | quantity | otype | risk_facts | value | currency | pos_value | pos_delta | pos_vega | |
|---|---|---|---|---|---|---|---|---|---|
| position | |||||||||
| 0 | option_pos_36 | 1 | American single | [ 1_jd] | 13.578 | EUR | 13.578 | -0.7310 | 12.7000 |
| 1 | option_pos_37 | 3 | European single | [ 2_jd] | 7.899 | EUR | 23.697 | 1.8531 | 41.3694 |
| 2 | option_pos_39 | 8 | American single | [ 3_sv] | 5.258 | EUR | 42.064 | -1.1560 | 28.3992 |
| 3 | option_pos_36 | 3 | American single | [ 4_sv] | 9.412 | EUR | 28.236 | -0.9552 | 12.9000 |
| 4 | option_pos_37 | 1 | American single | [ 5_gbm] | 4.869 | EUR | 4.869 | -0.3134 | 19.1000 |
| 5 | option_pos_36 | 5 | European single | [ 6_gbm] | 7.983 | EUR | 39.915 | 3.2050 | 88.8965 |
| 6 | option_pos_38 | 8 | European single | [ 7_jd] | 8.268 | EUR | 66.144 | 5.4696 | 112.6920 |
| 7 | option_pos_37 | 5 | American single | [ 8_gbm] | 7.171 | EUR | 35.855 | -1.8490 | 75.5000 |
| 8 | option_pos_36 | 8 | European single | [ 9_sv] | 1.619 | EUR | 12.952 | 2.2880 | 11.8480 |
| 9 | option_pos_37 | 1 | American single | [ 10_sv] | 6.759 | EUR | 6.759 | -0.2244 | -1.1000 |
| 10 | option_pos_39 | 2 | European single | [ 11_jd] | 8.092 | EUR | 16.184 | 1.2952 | 32.9850 |
| 11 | option_pos_38 | 2 | European single | [ 12_jd] | 19.790 | EUR | 39.580 | 1.8266 | 5.4426 |
| 12 | option_pos_36 | 2 | European single | [ 13_jd] | 9.280 | EUR | 18.560 | 1.2988 | 31.8768 |
| 13 | option_pos_38 | 4 | American single | [ 14_sv] | 11.752 | EUR | 47.008 | -1.6980 | 69.6000 |
| 14 | option_pos_39 | 4 | American single | [ 15_sv] | 8.032 | EUR | 32.128 | -1.0964 | 10.0000 |
| 15 | option_pos_37 | 9 | European single | [ 16_jd] | 24.939 | EUR | 224.451 | 7.2720 | 138.7152 |
| 16 | option_pos_39 | 4 | American single | [ 17_jd] | 10.172 | EUR | 40.688 | -1.7324 | 79.4228 |
| 17 | option_pos_39 | 9 | European single | [ 18_sv] | 17.568 | EUR | 158.112 | 7.1190 | 18.7866 |
| 18 | option_pos_39 | 2 | American single | [ 19_sv] | 4.875 | EUR | 9.750 | -0.3186 | 10.8080 |
| 19 | option_pos_38 | 4 | European single | [ 20_jd] | 19.812 | EUR | 79.248 | 3.4404 | 37.7796 |
| 20 | option_pos_36 | 5 | European single | [ 21_sv] | 26.103 | EUR | 130.515 | 4.4125 | 3.1945 |
| 21 | option_pos_38 | 2 | American single | [ 22_gbm] | 8.063 | EUR | 16.126 | -0.3744 | 42.2106 |
| 22 | option_pos_36 | 7 | American single | [ 23_gbm] | 0.000 | EUR | 0.000 | 0.0000 | 0.0000 |
| 23 | option_pos_37 | 4 | European single | [ 24_sv] | 2.052 | EUR | 8.208 | 1.3584 | 1.4144 |
| 24 | option_pos_38 | 9 | American single | [ 25_sv] | 6.286 | EUR | 56.574 | -2.0088 | 42.3000 |
| 25 | option_pos_38 | 2 | European single | [ 26_jd] | 4.641 | EUR | 9.282 | 1.3874 | 11.9626 |
| 26 | option_pos_37 | 8 | American single | [ 27_gbm] | 7.227 | EUR | 57.816 | -6.6688 | 47.2000 |
| 27 | option_pos_39 | 4 | American single | [ 28_gbm] | 13.154 | EUR | 52.616 | -2.0692 | 69.2000 |
| 28 | option_pos_37 | 3 | European single | [ 29_sv] | 24.595 | EUR | 73.785 | 2.5590 | 7.9071 |
| 29 | option_pos_39 | 9 | European single | [ 30_sv] | 1.039 | EUR | 9.351 | 1.7442 | 7.2072 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 970 | option_pos_39 | 5 | American single | [221_jd] | 8.027 | EUR | 40.135 | -1.7390 | 81.5000 |
| 971 | option_pos_37 | 7 | American single | [222_sv] | 4.879 | EUR | 34.153 | -0.5922 | 29.4000 |
| 972 | option_pos_38 | 3 | European single | [223_gbm] | 12.599 | EUR | 37.797 | 2.4066 | 51.7317 |
| 973 | option_pos_39 | 9 | European single | [224_jd] | 2.806 | EUR | 25.254 | 3.6153 | 98.2503 |
| 974 | option_pos_36 | 1 | American single | [225_jd] | 8.058 | EUR | 8.058 | -0.3558 | 14.2000 |
| 975 | option_pos_39 | 3 | American single | [226_sv] | 16.163 | EUR | 48.489 | -1.6116 | 11.7000 |
| 976 | option_pos_37 | 4 | American single | [227_sv] | 5.360 | EUR | 21.440 | -0.8412 | -3.6000 |
| 977 | option_pos_38 | 6 | American single | [228_jd] | 6.255 | EUR | 37.530 | -1.2480 | 115.8000 |
| 978 | option_pos_38 | 3 | American single | [229_sv] | 5.099 | EUR | 15.297 | -0.4770 | 17.8017 |
| 979 | option_pos_39 | 9 | European single | [230_sv] | 7.857 | EUR | 70.713 | 5.5701 | 27.9288 |
| 980 | option_pos_38 | 8 | European single | [231_gbm] | 12.771 | EUR | 102.168 | 7.4208 | 72.7384 |
| 981 | option_pos_36 | 4 | American single | [232_sv] | 3.572 | EUR | 14.288 | -0.6080 | 4.0000 |
| 982 | option_pos_39 | 8 | American single | [233_gbm] | 6.536 | EUR | 52.288 | -3.6968 | 177.6000 |
| 983 | option_pos_38 | 7 | American single | [234_jd] | 18.614 | EUR | 130.298 | -4.2105 | 100.8000 |
| 984 | option_pos_37 | 9 | European single | [235_gbm] | 17.922 | EUR | 161.298 | 8.8866 | 8.8677 |
| 985 | option_pos_38 | 5 | American single | [236_gbm] | 18.455 | EUR | 92.275 | -3.8060 | 59.8640 |
| 986 | option_pos_38 | 3 | European single | [237_jd] | 9.939 | EUR | 29.817 | 2.1753 | 35.0295 |
| 987 | option_pos_36 | 4 | American single | [238_gbm] | 0.055 | EUR | 0.220 | -0.0504 | 10.8000 |
| 988 | option_pos_38 | 8 | American single | [239_jd] | 1.820 | EUR | 14.560 | -0.9704 | 4.8000 |
| 989 | option_pos_37 | 3 | European single | [240_gbm] | 11.596 | EUR | 34.788 | 2.1351 | 58.1622 |
| 990 | option_pos_36 | 7 | European single | [241_jd] | 6.309 | EUR | 44.163 | 5.0596 | 51.7664 |
| 991 | option_pos_37 | 6 | American single | [242_sv] | 17.465 | EUR | 104.790 | -5.5194 | -19.8000 |
| 992 | option_pos_38 | 4 | European single | [243_sv] | 9.644 | EUR | 38.576 | 2.6004 | 12.8704 |
| 993 | option_pos_39 | 9 | European single | [244_sv] | 9.115 | EUR | 82.035 | 5.8473 | 14.8833 |
| 994 | option_pos_37 | 7 | European single | [245_gbm] | 17.931 | EUR | 125.517 | 5.5713 | 145.7428 |
| 995 | option_pos_36 | 9 | American single | [246_jd] | 1.776 | EUR | 15.984 | -0.8289 | 39.6000 |
| 996 | option_pos_37 | 9 | European single | [247_jd] | 12.570 | EUR | 113.130 | 6.4656 | 145.0233 |
| 997 | option_pos_37 | 5 | American single | [248_sv] | 4.117 | EUR | 20.585 | -0.8575 | 5.0000 |
| 998 | option_pos_37 | 3 | European single | [249_sv] | 4.877 | EUR | 14.631 | 1.5633 | 8.1591 |
| 999 | option_pos_37 | 8 | American single | [250_jd] | 9.922 | EUR | 79.376 | -2.8024 | 140.0568 |
1000 rows × 9 columns
Single Option Valuation¶
We take out a single option from the portfolio and have a closer look.
option = port_sequ.valuation_objects[5]
option
<dx.dx_valuation.valuation_mcs_european_single at 0x10a446a50>
A plot of ten paths of the underlying risk factor.
option.underlying
<dx.dx_models.geometric_brownian_motion at 0x10a2bfed0>
paths = option.underlying.get_instrument_values()[:, :10]
plt.figure(figsize=(9, 5)), plt.grid()
plt.plot(option.underlying.time_grid, paths, 'b')
plt.ylabel('risk factor level');
Valuation of the option and Greeks.
option.present_value()
7.982793
option.delta()
0.641
option.vega()
17.7793
Deriving values, deltas and vegas for different initial values.
%%time
S0 = option.underlying.initial_value
s_list = np.arange(S0 - 8, S0 + 8.1, 2.)
pv = []; de = []; ve = []
for s in s_list:
option.update(s)
pv.append(option.present_value())
de.append(option.delta(.5))
ve.append(option.vega(0.2))
CPU times: user 10.1 s, sys: 354 ms, total: 10.5 s Wall time: 4.96 s
Plotting the results.
plot_option_stats(s_list, pv, de, ve)
Risk Analysis¶
Full distribution of portfolio present values illustrated via histogram.
%time pvs = port_sequ.get_present_values()
CPU times: user 4min 13s, sys: 17.2 s, total: 4min 30s Wall time: 2min 19s
plt.figure(figsize=(9, 6)); plt.hist(pvs, bins=30);
plt.xlabel('portfolio present values');plt.ylabel('frequency'); plt.grid()
Some statistics via pandas.
pdf = pd.DataFrame(pvs, columns=['values'])
pdf.describe()
| values | |
|---|---|
| count | 1000.000000 |
| mean | 48052.581112 |
| std | 4506.642731 |
| min | 35194.008630 |
| 25% | 44796.433598 |
| 50% | 47711.788468 |
| 75% | 50807.405837 |
| max | 68172.669032 |
The delta risk (sensitivities) report.
%%time
deltas = port_sequ.get_port_risk(Greek='Delta', fixed_seed=True, step=0.2,
risk_factors=risk_factors.keys()[:4])
risk_report(deltas)
39_jd_Delta
0.8 1.0 1.2
factor 37.52 46.91 56.29
value 9508.56 9535.46 9564.57
107_sv_Delta
0.8 1.0 1.2
factor 24.43 30.54 36.65
value 9543.92 9535.21 9530.26
144_sv_Delta
0.8 1.0 1.2
factor 21.36 26.70 32.04
value 9532.42 9534.82 9540.26
246_jd_Delta
0.8 1.0 1.2
factor 44.73 55.91 67.09
value 9531.09 9534.45 9542.52
CPU times: user 1min 38s, sys: 651 ms, total: 1min 39s
Wall time: 1min 37s
The vega risk (sensitivities) report.
%%time
vegas = port_sequ.get_port_risk(Greek='Vega', fixed_seed=True, step=0.2,
risk_factors=risk_factors.keys()[:4])
risk_report(vegas)
39_jd_Vega
0.8 1.0 1.2
factor 0.49 0.61 0.73
value 9526.82 9534.45 9541.80
107_sv_Vega
0.8 1.0 1.2
factor 0.28 0.35 0.42
value 9533.79 9534.45 9535.03
144_sv_Vega
0.8 1.0 1.2
factor 0.50 0.62 0.75
value 9533.32 9534.45 9535.83
246_jd_Vega
0.8 1.0 1.2
factor 0.21 0.26 0.32
value 9532.91 9534.45 9537.26
CPU times: user 1min 40s, sys: 627 ms, total: 1min 41s
Wall time: 1min 39s
Visualization of Selected Results¶
Selected results visualized.
res[['pos_value', 'pos_delta', 'pos_vega']].hist(bins=30, figsize=(9, 6))
plt.ylabel('frequency')
<matplotlib.text.Text at 0x109ad73d0>
Sample paths for three underlyings.
paths_0 = port_sequ.underlying_objects.values()[0]
paths_0.generate_paths()
paths_1 = port_sequ.underlying_objects.values()[1]
paths_1.generate_paths()
paths_2 = port_sequ.underlying_objects.values()[2]
paths_2.generate_paths()
An the resulting plot.
pa = 5; plt.figure(figsize=(10, 6))
plt.plot(port_sequ.time_grid, paths_0.instrument_values[:, :pa], 'b');
plt.plot(port_sequ.time_grid, paths_1.instrument_values[:, :pa], 'r.-');
plt.plot(port_sequ.time_grid, paths_2.instrument_values[:, :pa], 'g-.', lw=2.5);
print 'Paths for %s (blue)' % paths_0.name
print 'Paths for %s (red)' % paths_1.name
print 'Paths for %s (green)' % paths_2.name; plt.grid()
plt.ylabel('risk factor level'); plt.gcf().autofmt_xdate()
Paths for 107_sv (blue) Paths for 144_sv (red) Paths for 39_jd (green)
Books¶
By others:
- Python for Financial Modelling @ Wiley Finance (2009)
- Python for Finance @ Packt Publishing (2014)
By myself:
- Python for Finance – Analyze Big Financial Data @ O'Reilly (2014)
- Derivatives Analytics with Python @ Wiley Finance (2015)
Available as ebook and from December 2015 as print version.

Forthcoming 2015 at Wiley Finance ...

Meetups¶
For Python Quants Conference¶
- 1st conference in New York City on 14. March 2014
- 2nd conference in London on 28. November 2014
- 3rd conference planned for QI 2015 in Asia (eg Shanghai)
Final Thoughts¶
My wish for Python in the future: to become THE glue language and platform for
- data analytics
- financial analytics (derivatives, risk)
- development efforts in general
- performance technologies
- science and the technology world
- ...
Contact us¶
Please contact us if you have any questions or want to get involved in our Python community events.

Python Quant Platform | http://quant-platform.com
Derivatives Analytics with Python | Derivatives Analytics @ Wiley Finance
Python for Finance | Python for Finance @ O'Reilly